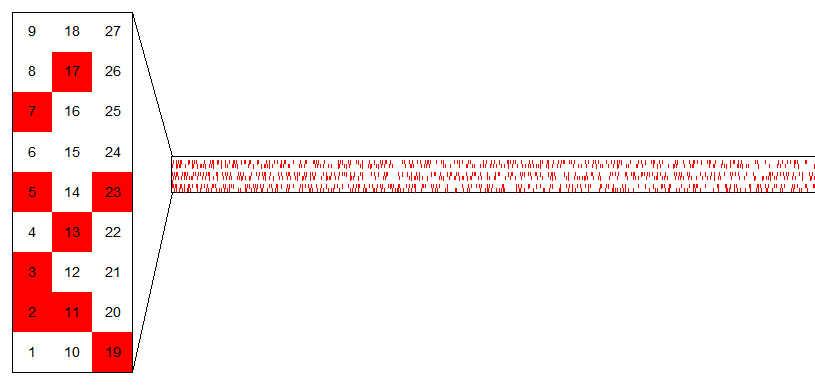
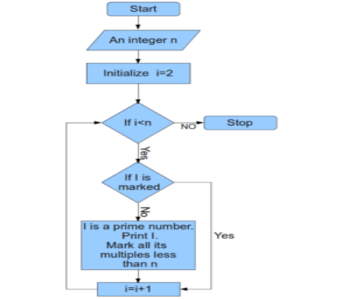
outletkerop.blogg.se - New prime number generator algorithm

NEW PRIME NUMBER GENERATOR ALGORITHM CODE
NEW PRIME NUMBER GENERATOR ALGORITHM TRIAL

Overcoming memory constraint by using Paging, Clusters of machine and finding prime numbers quickly up to cryptographic standard.Ĭopy Code private static int FindPrimeUsingSieveOfEratosthenesOptimised( int topCandidate = 1000000).

More efficient implementation of all the algorithm.

Unnecessary calculation but also difficult to comprehend. In the code attached a optimized implementation is provided which will ignore Unnecessary since the result is above 10.This cant be removed in a normal implementation. Performed for all the number less than square root of the 10 which is 3. Lets say we need to find all the prime under 10. The reason being unnecessary computation performed for numbers which are not The above code is efficient than Eratosthenes and inefficient or same as Return (totalCount + 2) // 2 and 3 will be missed in Sieve Of Atkins IsPrime = !isPrime įor ( int z = k z <= topCandidate z += k) If ((computedVal <= topCandidate) & (computedVal % 12 = 11)) Int squareRoot = ( int)Math.Sqrt(topCandidate) Below is the optimized implementation of the SOS.īitArray isPrime = new BitArray(topCandidate + 1) Sieve which has value true is multiplied by 2 and incremented by 1 to give the prime number. While (thisFactor * thisFactor = 1 and less than = i and less than n * Mark all the non-primes */ int thisFactor = 2 * Set all but 0 and 1 to prime status */ Multiple is greater than 10.The prime numbers are 2, 3, 5, and 7.īitArray myBA1 = new BitArray(topCandidate + 1) This process is continues until the multiple of the number is less than 10.įinally all the index of the boolean array which has value true is considered as Prime except index 1.

Starting from 2,the multiples of two are set to false in the array. In order to find prime number less than 10, a boolean array of length 10 is created which has values true for all. Sieve of Eratosthenes is the ancient algorithm to find the prime number and is the first TotalCount is initialized to 1 since 2 is prime number and ignored in our code.įor ( long i = 3 i < topCandidate i += 2) In order to find whether a number is prime or not the number is divided by odd number and checked for remainder starting from 3 up to odd number whose square is less than the number we are checking.Īvailable then the number is not prime otherwise it is.

NEW PRIME NUMBER GENERATOR ALGORITHM TRIAL

Using the code Brute Force Method or Trial Divisionīrute Force method is the easiest method to find the prime number. This "harder to factorize" prime number problem is used as a one-way function for the basis of PKC. If the number given is a 128 digit number ,then it is hard to find the factors quickly. Let's take two prime number 7 and 13 and if I want to calculate the product, we can calculate it easily which is 91.Now,instead let's say I have number 91 and I want to find the pair of prime numbers whose product will give 91 It will be harder to find but we can find it eventually. Instead of going too deep into PKC, let me give the how prime numbers are used. Prime numbers are the basis for the "Public Key Cryptography (PKC)". This articleĭoesn't talk about the algorithm itself but optimized implementation of the algorithm. C++ and Java implementations.This article explains in detail about generating prime numbers using the four well known algorithm. Sieve of Eratosthenes illustrated explanation.If you are looking for only prime numbers you can generate them and keep adding them to a list.You can use bitmaps to pack the memory.There is no need to store even numbers, as there is only one even prime number.This algorithm is usually what is meant when "the sieve of Eratosthenes" is mentioned. The Prime Sieve of Eratosthenes algorithm precalculates from the bottom up - given a table of N ] to false ("cross it out")